Чему равен и как найти косинус угла в треугольнике?

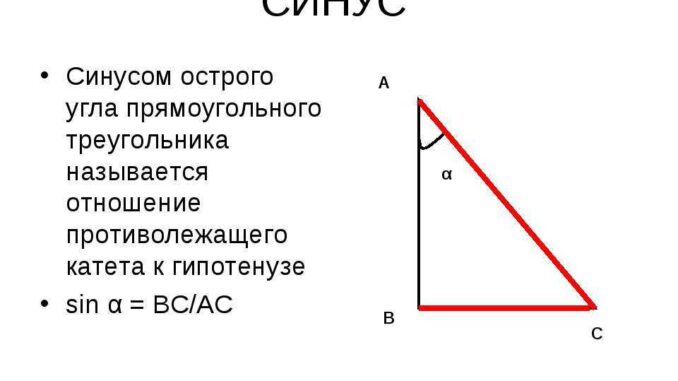
Косинус угла в треугольнике является одним из основных тригонометрических понятий. Он позволяет выяснить отношение длины стороны треугольника к длинам других его сторон. Косинус угла равен отношению длины прилегающего к углу катета к гипотенузе треугольника.

Для нахождения косинуса угла необходимо знать длины сторон треугольника и определить нужный угол. Формула для расчета косинуса угла основывается на использовании теоремы Пифагора:

cos(angle) = adjacent side / hypotenuse.

Применяя эту формулу в практике, можно получить значение косинуса угла и использовать его для решения различных задач, связанных с треугольником. Косинус является базовым инструментом для нахождения других тригонометрических функций, таких как синус и тангенс.

Определение и значение косинуса

Косинус угла — это геометрическое значение, определяемое отношением длины прилегающего катета к гипотенузе прямоугольного треугольника. Косинус угла обозначается как cos и может быть выражен числом от -1 до 1.

Значение косинуса угла зависит от величины самого угла. Если угол равен 0 градусов, то косинус будет равен 1, так как прилегающий катет совпадает с гипотенузой. Если угол равен 90 градусов, то косинус будет равен 0, так как прямой угол не имеет прилегающего катета.

Значение косинуса также можно использовать для определения сходства или различия между двумя векторами в пространстве. Чем ближе косинус угла между векторами к единице, тем больше сходство между ними.

Косинус угла находит применение в различных областях, таких как тригонометрия, геометрия, физика, компьютерная графика и другие. Он является важным математическим понятием, позволяющим решать различные задачи и проводить анализ данных.

Применение косинуса в треугольниках

Косинус угла в треугольнике является одним из основных тригонометрических отношений, рассматриваемых при изучении геометрии и математики. Он широко применяется для вычисления длины сторон и углов треугольников, а также для решения различных задач в геодезии, физике и других науках.

Формула для вычисления косинуса угла

Косинус угла в треугольнике (найдите градус угла abc) определяется отношением длин двух его сторон к длине третьей стороны. Формула для вычисления косинуса угла имеет следующий вид:

cos(A) = (b² + c² — a²) / (2bc)

где A — угол треугольника, a, b, c — длины сторон треугольника.

Примеры применения косинуса угла в треугольниках

Применение косинуса угла возможно в различных задачах. Например, если известны длины двух сторон и величина угла между ними, можно вычислить длину третьей стороны треугольника с помощью формулы косинуса. Также с помощью косинуса можно найти величину угла треугольника, если известны длины всех его сторон. Для этого необходимо использовать обратную функцию косинуса.

Косинус угла также применяется в геодезии для определения расстояний между точками на земной поверхности. Зная координаты двух точек и угол между направлением на север и линией, соединяющей эти точки, можно вычислить расстояние между ними с помощью формулы косинуса.

Таким образом, косинус угла в треугольнике находит применение в различных областях и является неотъемлемой частью изучения и решения задач связанных с треугольниками.

Тригонометрический круг и косинус

Тригонометрический круг является основным инструментом для изучения тригонометрии. Он представляет собой окружность, разделенную на 360 градусов или 2π радиан. В центре круга находится начало координат, а на окружности отмечены основные углы и точки, соответствующие значениям тригонометрических функций.

Косинус — это одна из основных тригонометрических функций, которая определяется как отношение прилежащего катета к гипотенузе прямоугольного треугольника. В тригонометрическом круге, косинус угла определяется как значение координаты по оси x для точки, соответствующей данному углу.

Формула нахождения косинуса угла

Формула нахождения косинуса угла в прямоугольном треугольнике:

cos(α) = a / c,

где α — угол между гипотенузой и прилегающим катетом, a — длина прилегающего катета, c — длина гипотенузы.

В тригонометрическом круге косинус угла определяется координатой по оси x для точки на окружности, соответствующей данному углу.

Таким образом, для нахождения косинуса угла нужно либо использовать формулу в прямоугольном треугольнике, либо найти соответствующую точку на тригонометрическом круге и вычислить значение координаты по оси x.

Геометрическая интерпретация косинуса

Косинус угла в треугольнике можно интерпретировать геометрически. Рассмотрим треугольник ABC, в котором угол A острый, стороны a, b и c соответственно противолежащие углам A, B и C.

Теорема косинусов утверждает, что квадрат одной стороны треугольника равен сумме квадратов двух других сторон, умноженных на косинусы соответствующих противолежащих углов.

То есть, косинус угла A можно найти как отношение длины стороны b к гипотенузе c:

cos(A) = b / c

Зная длины сторон треугольника, можно вычислить косинусы углов и использовать их при решении задач геометрии, механики, физики и других наук.

Тригонометрические преобразования для вычисления косинуса

Косинус угла в треугольнике является одним из основных тригонометрических значений, которое позволяет определить соотношение между длинами сторон треугольника и значениями его углов. Для вычисления косинуса угла необходимо знать длины двух сторон треугольника и угол между ними.

Формула для вычисления косинуса угла:

cos A = (b^2 + c^2 — a^2) / (2bc)

В этой формуле a, b и c обозначают длины сторон треугольника, а A обозначает угол между сторонами b и c.

Для вычисления косинуса угла необходимо знать значения длин сторон треугольника, которые могут быть измерены с помощью линейки или вычислены с использованием других известных значений и формул. После определения длин сторон и угла, можно использовать формулу для вычисления косинуса и получить значение этого тригонометрического значения.

Вычисление косинуса угла может быть полезно при решении различных задач физики, геометрии, астрономии и других наук. Косинус угла может использоваться для определения расстояний, направлений движения, углов поворотов и других параметров в различных системах и задачах.

Нахождение косинуса угла в прямоугольном треугольнике

В прямоугольном треугольнике косинус угла может быть определен по одному из его катетов и гипотенузе.

Для нахождения косинуса угла α, применим следующую формулу:

cos(α) = adjacent / hypotenuse

Здесь adjacent — это длина стороны прямоугольного треугольника, прилегающей к данному углу, а hypotenuse — это длина гипотенузы треугольника.

Например, если известно, что adjacent равен 3, а hypotenuse равен 5, то косинус угла α может быть вычислен как:

cos(α) = 3 / 5

таким образом, косинус угла α будет равен 0.6.

Косинус угла является числовым значением, которое может быть использовано для решения различных задач, связанных с прямоугольными треугольниками. Например, можно использовать косинус угла для нахождения длины неизвестной стороны треугольника или для нахождения угла между двумя сторонами треугольника.

Нахождение косинуса угла в непрямоугольном треугольнике

Косинус угла в непрямоугольном треугольнике можно найти с помощью формулы косинусов. Формула косинусов позволяет найти косинус любого угла треугольника, если известны длины сторон этого треугольника.

Формула косинусов выглядит следующим образом:

cos(α) = (b² + c² — a²) / (2bc)

Где:

• α — угол треугольника
• a — длина стороны треугольника, противолежащей углу α
• b и c — длины других сторон треугольника

Для нахождения косинуса угла в непрямоугольном треугольнике необходимо знать длины всех трех сторон треугольника. С помощью формулы косинусов можно вычислить косинус угла и использовать это значение в дальнейших расчетах или анализе треугольника.

Формула косинусов очень полезна при решении различных задач, связанных с геометрией и тригонометрией, таких как вычисление площади треугольника или нахождение углов треугольника по известным сторонам.

Примеры расчета косинуса угла в треугольниках

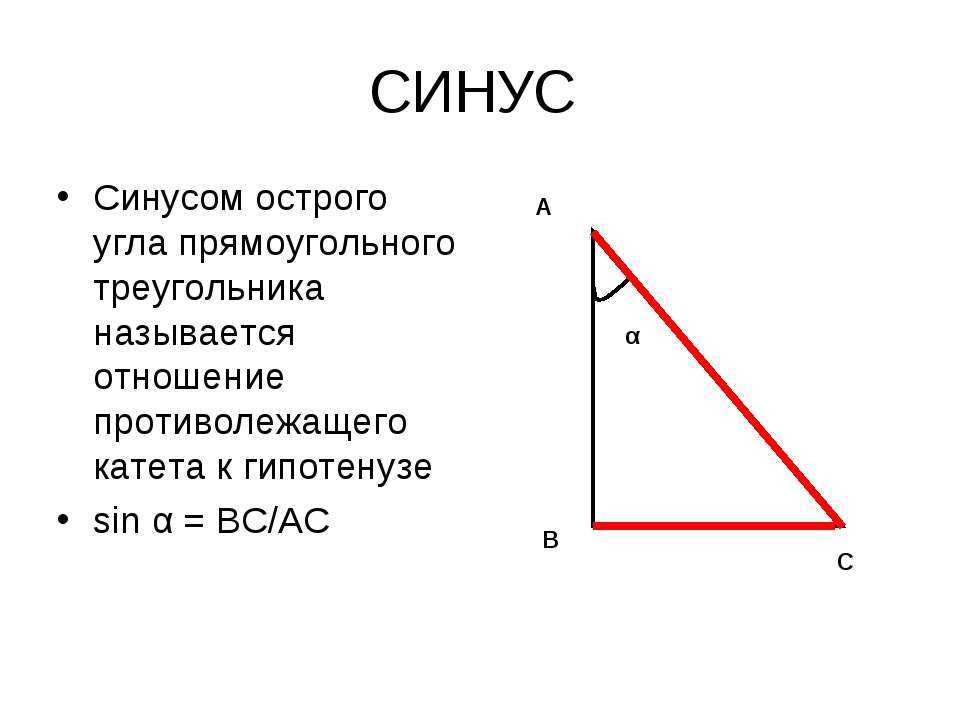
Для расчета косинуса угла в треугольнике можно использовать теорему косинусов. Эта теорема устанавливает связь между длинами сторон треугольника и косинусом одного из его углов.

Пример 1:

Пусть у нас есть треугольник ABC, где стороны AC и BC равны 5 и 9 соответственно, а угол ABC составляет 60 градусов. Чтобы найти косинус этого угла, мы можем использовать теорему косинусов, где квадрат длины стороны AB будет равен сумме квадратов длин сторон AC и BC минус удвоенное произведение длин этих сторон на косинус угла ABC.

Таким образом, мы можем записать это в виде уравнения:

c² = a² + b² — 2ab * cos(C)

Подставляя значения, получим:

c² = 5² + 9² — 2 * 5 * 9 * cos(60)

Вычисляя, получаем:

c² = 25 + 81 — 90 * cos(60)

c² = 106 — 90 * 0.5

c² = 61

Таким образом, длина стороны AB равна корню квадратному из 61, что примерно равно 7.81. Для нахождения косинуса угла ABC нам нужно разделить длину стороны AB на произведение длин сторон AC и BC.

cos(60) = AB / (AC * BC)

Подставляя значения:

cos(60) = 7.81 / (5 * 9)

Вычисляя, получаем:

cos(60) ≈ 0.173

Пример 2:

Пусть у нас есть треугольник XYZ, где стороны XY, YZ и XZ равны 8, 6 и 4 соответственно. Чтобы найти косинус угла YXZ, мы также можем использовать теорему косинусов.

Запишем уравнение теоремы косинусов для треугольника XYZ:

y² = x² + z² — 2xz * cos(Y)

Подставляя значения, получим:

y² = 8² + 4² — 2 * 8 * 4 * cos(Y)

Вычисляя, получаем:

y² = 64 + 16 — 64 * cos(Y)

y² = 80 — 64 * cos(Y)

Таким образом, длина стороны YX равна корню квадратному из 80 минус 64 умноженного на косинус угла YXZ.

Для нахождения косинуса угла YXZ, мы можем использовать соотношение:

cos(Y) = (x² + y² — z²) / (2xy)

Подставляя значения, получим:

cos(Y) = (8² + y² — 4²) / (2 * 8 * y)

Вычисляя, получаем:

cos(Y) = (64 + y² — 16) / (16 * y)

cos(Y) = (y² + 48) / (16y)

Таким образом, мы нашли косинус угла YXZ, используя теорему косинусов и соотношение для косинуса.

Видео:

Косинус угла между векторами. Коллинеарность векторов

Косинус угла между векторами. Коллинеарность векторов by Tatyana Grygoryeva 2 years ago 8 minutes, 22 seconds 10,273 views https://www.youtube.com/embed/NK7fQDRjVXU

Вопрос-ответ:

Как определить косинус угла в треугольнике?

Косинус угла в треугольнике можно определить, используя формулу косинусов: cos(A) = (b^2 + c^2 — a^2) / (2bc), где A — угол при стороне a, b и c — длины сторон треугольника.

Как найти косинус угла в прямоугольном треугольнике?

В прямоугольном треугольнике косинус угла можно найти, используя соотношение катетов и гипотенузы: cos(A) = adjacent/hypotenuse, где A — угол, adjacent — длина прилежащего к углу A катета, hypotenuse — длина гипотенузы.

Как найти косинус угла, если известны координаты вершин треугольника в декартовой системе координат?

Если известны координаты вершин треугольника в декартовой системе координат, косинус угла можно найти, используя координаты векторов, образованных сторонами треугольника. Косинус угла между векторами a и b равен: cos(A) = (a • b) / (|a| * |b|), где A — угол, a и b — векторы, • — операция скалярного произведения, |a| и |b| — длины векторов.