Основы геометрии: что такое треугольник и углы треугольника?

Геометрия – это раздел математики, который изучает фигуры, их свойства и взаимные отношения. Одной из основных фигур в геометрии является треугольник.

Треугольник – это плоская фигура, образованная тремя отрезками, называемыми сторонами. У треугольника есть три вершины и три угла. В зависимости от длин сторон треугольник может быть равносторонним, равнобедренным или разносторонним.

В геометрии особое внимание уделяется изучению углов треугольника. Углы треугольника – это углы, образованные двумя сторонами треугольника.

Сумма углов треугольника всегда равна 180 градусов. Угол, образованный двумя сторонами треугольника, называется внутренним углом. Также существуют внешние углы треугольника, которые образуются продолжением сторон треугольника.

Треугольник – это не только основа для изучения геометрии, но и является одной из самых распространенных и уникальных форм в природе и архитектуре.

Основы геометрии: треугольники и их углы

Треугольник — полигон с тремя сторонами

В геометрии треугольник — это полигон, который имеет всего три стороны и три вершины. Он является одной из самых основных фигур и встречается во многих задачах и заданиях. Каждая сторона треугольника соединяет две вершины, а углы треугольника образованы пересечением его сторон.

Углы треугольника

В треугольнике образуются три угла, которые называются внутренними углами. Сумма углов треугольника всегда равна 180 градусов. Каждый из углов может быть разным по величине и характеристикам:

• Острый угол: угол, меньший 90 градусов. Он имеет острый пик и называется острым из-за своей формы.
• Прямой угол: угол, равный 90 градусам. Он образуется, когда одна из сторон треугольника перпендикулярна другой.
• Тупой угол: угол, больший 90 градусов. Он имеет тупой пик и называется тупым из-за своей формы.
• Разносторонний треугольник: треугольник, у которого все три стороны имеют разные длины. В этом случае все углы треугольника также будут разными.
• Равнобедренный треугольник: треугольник, у которого две стороны и два угла равны. Такой треугольник имеет две равные стороны и два равных угла.

Углы и стороны треугольника часто используются при решении задач, а также в повседневной жизни, например, при строительстве или изображении фигур на плоскости. Знание основ геометрии поможет вам разобраться с треугольником и его углами и использовать их для решения различных задач.

Что такое геометрия

Геометрия — это раздел математики, который изучает фигуры, их свойства и отношения между ними. Основы геометрии были заложены в древней Греции, и с тех пор она стала одной из важнейших наук.

Геометрия рассматривает различные фигуры, такие как треугольники, квадраты, окружности и др., и исследует их основные свойства. Основными понятиями в геометрии являются точка, прямая и плоскость.

Геометрия также изучает углы, которые являются важной частью многих фигур. Углы могут быть острыми, прямыми, тупыми или полными, и их величина измеряется в градусах.

Геометрия имеет широкое применение как в научных исследованиях, так и в повседневной жизни. Например, строители используют геометрию для правильного расположения стен и перегородок, а дизайнеры используют ее для создания эстетически привлекательных форм.

В общем, геометрия помогает нам лучше понимать фигуры и пространство вокруг нас, и находит применение во многих областях нашей жизни.

Определение треугольника

Треугольник — это геометрическая фигура, состоящая из трех отрезков, называемых сторонами. Стороны треугольника соединены в трех вершинах, образуя три угла. Каждый угол треугольника (дано ab bc найти углы треугольника) образуется двумя его сторонами и является местом пересечения этих сторон. Таким образом, треугольник — это трехугольная плоская фигура.

Особенности треугольника:

• Треугольник имеет три стороны и три угла.
• Сумма всех углов треугольника равна 180 градусов.
• Сумма длин любых двух сторон треугольника всегда больше, чем длина третьей стороны.
• Если все стороны треугольника имеют одинаковую длину, то такой треугольник называется равносторонним.
• Если только две стороны треугольника имеют одинаковую длину, то такой треугольник называется равнобедренным.
• Если все углы треугольника острые (меньше 90 градусов), то такой треугольник называется остроугольным.
• Если один угол треугольника равен 90 градусов, то такой треугольник называется прямоугольным.
• Если один угол треугольника больше 90 градусов, то такой треугольник называется тупоугольным.

Треугольники имеют широкое применение в геометрии, а также во многих других областях, таких как архитектура, строительство, физика и другие.

Структура треугольника

Треугольник — это геометрическая фигура, образованная тремя отрезками, называемыми сторонами. У треугольника есть три вершины, которые соединяются сторонами.

Стороны треугольника

Стороны треугольника образуют его основные элементы. Три стороны обозначаются буквами a, b и c, их длины могут быть различными. Сумма длин любых двух сторон треугольника всегда будет больше длины третьей стороны.

Вершины треугольника

Вершины треугольника обозначаются заглавными буквами A, B и C. Они определяют положение и форму треугольника. Каждая вершина соединена с двумя другими вершинами сторонами треугольника. Место пересечения сторон называется углом треугольника и обозначается буквами A, B и C в соответствии с вершиной.

Углы треугольника

Углы треугольника образуются между сторонами. Треугольник имеет три угла, обозначаемые буквами α, β и γ. Сумма углов треугольника всегда равна 180 градусам. Углы могут быть остроугольными, прямыми или тупоугольными, в зависимости от их величины.

Таким образом, структура треугольника включает в себя стороны, вершины и углы. Изучение этих элементов позволяет анализировать и определять свойства треугольников и решать различные задачи в геометрии.

Различные типы треугольников

Треугольник – это геометрическая фигура, состоящая из трех отрезков, которые называются сторонами, и трех углов, которые образуются между этими сторонами. Треугольники могут быть различных типов, в зависимости от длин сторон и величины углов.

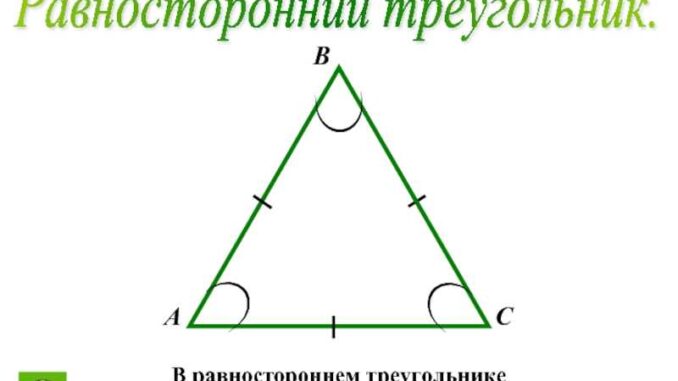
Равносторонний треугольник

Равносторонний треугольник – это треугольник, у которого все стороны и все углы равны между собой. Такой треугольник имеет три равные стороны и три равных угла, которые составляют по 60 градусов.

Равнобедренный треугольник

Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой. Углы при основании равнобедренного треугольника всегда равны между собой, а третий угол может быть разным.

Прямоугольный треугольник

Прямоугольный треугольник – это треугольник, у которого один из углов является прямым (90 градусов). Сторона, противолежащая прямому углу, называется гипотенузой, а две другие стороны — катетами.

Разносторонний треугольник

Разносторонний треугольник – это треугольник, у которого все стороны разные. Углы разностороннего треугольника также могут быть разными величинами.

Таким образом, существуют различные типы треугольников, которые отличаются по длине сторон и величине углов. Знание этих типов позволяет более точно классифицировать и описывать треугольники в геометрии.

Углы треугольника

Углы треугольника — это основные элементы, определяющие его форму и уникальные свойства. Вся сумма углов треугольника равна 180 градусов.

Виды углов треугольника:

1. Прямой угол: Прямой угол в треугольнике равен 90 градусов. Он обозначается символом ∠.

2. Острый угол: Острый угол в треугольнике меньше 90 градусов. Он обозначается символом ∠.

3. Тупой угол: Тупой угол в треугольнике больше 90 градусов, но меньше 180 градусов. Он обозначается символом ∠.

Свойства углов треугольника:

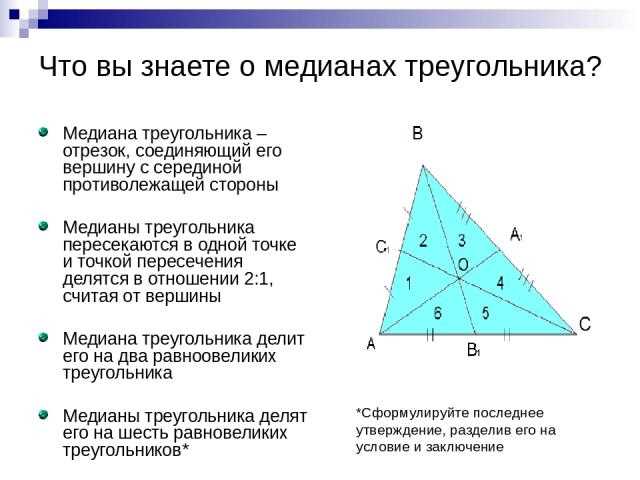
1. Сумма углов треугольника: Сумма всех углов треугольника равна 180 градусам. Это основное свойство, которое можно использовать для нахождения значения недостающего угла.

2. Углы вокруг точки: Углы, образованные сторонами треугольника, в сумме составляют 360 градусов. Это означает, что если мы возьмем точку и соединим ее с вершинами треугольника, то углы, образованные этими линиями, в сумме будут равны 360 градусам.

3. Углы смежных сторон: Углы, прилегающие к одной стороне треугольника, называются смежными углами. Сумма смежных углов всегда равна 180 градусам.

Примеры использования:

Например, если в треугольнике известно два угла, мы можем найти третий, вычитая сумму известных углов из 180 градусов.

Также, зная углы вокруг точки, можно рассчитать угол в треугольнике, если один из углов вокруг точки и угол треугольника прилегают к одной и той же вершине.

Понимание свойств и видов углов треугольника помогает понять его структуру и решать задачи на нахождение углов и сторон треугольника.

Углы внутри треугольника

У треугольника есть три внутренних угла. Каждый из этих углов образуется двумя сторонами треугольника. Сумма всех углов в треугольнике всегда равна 180 градусам.

Вершина треугольника — это точка пересечения трех сторон. От вершины идут две стороны, образуя углы. Углы треугольника обозначаются буквами, например, угол А, угол В, угол С. Обычно угол А находится против стороны BC, угол В — против стороны AC, а угол С — против стороны AB.

Внешние углы треугольника — это углы, образованные продолжением сторон треугольника за его вершинами. Внешний угол треугольника всегда больше суммы двух его внутренних углов, которые прилегают к этому внешнему углу.

Сумма углов в треугольнике всегда равна 180 градусам. Это правило называется теоремой о сумме углов треугольника. Если известны два угла треугольника, то третий угол можно найти, отняв сумму из 180 градусов. Например, если угол А равен 60 градусам, а угол В равен 40 градусам, то угол С можно найти, отняв 60 + 40 = 100 градусов от 180 градусов.

Углы на прямой и вокруг треугольника

Углы на прямой — это пара смежных углов, которые образуют линию. Они располагаются по одну сторону линии и дополняют друг друга до полных 180 градусов. Например, если у нас есть угол A и угол B на прямой, то они будут смежными углами. Если угол А равен 50 градусам, то угол В будет равен 130 градусам, так как они дополняют друг друга до 180 градусов.

Углы вокруг треугольника — это углы, которые образуются при соединении вершин треугольника со внешними точками. В сумме они также равны 360 градусов. Например, если у нас есть треугольник ABC, и мы проведем линии из вершин A, B и C к точкам D, E и F соответственно, то углы BAD, CBE и ACF будут углами вокруг треугольника.

Чтобы вычислить углы вокруг треугольника, можно использовать формулу: сумма углов вокруг треугольника равна 360 градусов. Эта формула является консеквенцией суммы углов треугольника, которая равна 180 градусов. Таким образом, можно сказать, что каждая из вершин треугольника «отнимает» от общей суммы углов вокруг треугольника по 180 градусов.

Свойства треугольников и их углов

Треугольник — это геометрическая фигура, состоящая из трех сторон и трех углов. У треугольника есть несколько свойств, которые помогают нам классифицировать его и изучать его особенности.

Сумма углов треугольника

Одно из основных свойств треугольника заключается в том, что сумма всех его углов равна 180 градусам. Это значит, что если мы знаем значения двух углов треугольника, мы можем легко найти третий угол путем вычитания суммы из 180 градусов.

Виды треугольников по длинам сторон

Треугольники можно классифицировать по длинам их сторон. Равносторонний треугольник имеет три равные стороны, равнобедренный треугольник имеет две равные стороны, а разносторонний треугольник имеет все стороны разной длины.

Виды треугольников по величине углов

Треугольники также могут быть классифицированы по величине их углов. Остроугольный треугольник имеет все углы меньше 90 градусов, тупоугольный треугольник имеет один угол больше 90 градусов, а прямоугольный треугольник имеет один угол равный 90 градусов.

Теорема углов треугольника

Еще одно важное свойство треугольника — это теорема углов треугольника. Согласно этой теореме, сумма двух углов треугольника всегда больше третьего угла. Например, если два угла треугольника равны 45 и 60 градусов, то третий угол должен быть меньше 75 градусов.

Изучая свойства треугольников и их углов, мы можем легче анализировать и решать геометрические задачи, а также строить и классифицировать треугольники по их особенностям.

Видео:

Треугольники. 7 класс.

Треугольники. 7 класс. by МЕКТЕП OnLine ГЕОМЕТРИЯ 2 years ago 10 minutes, 27 seconds 29,623 views https://www.youtube.com/embed/PZFM7e7MDtU

Что такое угол? Виды углов: прямой, острый, тупой, развернутый угол

Что такое угол? Виды углов: прямой, острый, тупой, развернутый угол by Ваш Учитель 1 year ago 6 minutes, 59 seconds 60,608 views https://www.youtube.com/embed/LTEW7Pw93Gg

Вопрос-ответ:

Как определить понятие треугольника?

Треугольник — это геометрическая фигура, состоящая из трех прямых отрезков, называемых сторонами, и трех точек, где стороны пересекаются, называемых вершинами. Треугольник имеет три угла, сумма которых равна 180 градусам.

Какие бывают виды треугольников?

Существует несколько видов треугольников в зависимости от их сторон и углов. Равносторонний треугольник имеет три равные стороны. Равнобедренный треугольник имеет две равные стороны и два равных угла. Прямоугольный треугольник имеет один прямой угол, который составляет 90 градусов. Остроугольный треугольник имеет три острых угла, а тупоугольный треугольник имеет один тупой угол, который превышает 90 градусов.